Лекция по методике математики 4 курс
Мальцева Е. , доцент кафедры методики начального образования, канд. пед. наук

1) Дети посадили около школы 5 берез, а лип на 3 больше, чем берез. Сколько лип посадили дети около школы?
2) 15 конфет раздали 3 детям поровну. По сколько конфет получил каждый из детей?
3) В первый день в киоске было продано 5 журналов, а во второй – на 3 журнала больше. Сколько журналов было продано за два дня?
4) На автостоянке 5 грузовых машин, а легковых в 3 раза больше. Сколько всего машин на стоянке?
5) На пошив 5 платьев идет 15м материи. Сколько метров ткани нужно для пошива 8 таких платьев?
6) За 7 тетрадей в клетку и 5 тетрадей в линейку по одинаковой цене Катя заплатила 72 рубля. Сколько стоят тетради в клетку и в линейку по отдельности?
7) У Кати было 36 р. За завтрак она заплатила 1/4 имеющихся у нее денег. Сколько стоил завтрак?

Методика ознакомления с долями и дробями

Методика ознакомления с образованием, названием, записью и сравнением долей. Ознакомление с методикой решения задач на нахождение доли от числа и числа по его доле. Методика ознакомления с образованием, названием, записью и сравнением дробей. Ознакомление с методикой решения задач на нахождение дроби от числа и числа по его дроби. Особенности методики изучения долей и дробей в вариативных программах начального курса математики.

Методика ознакомления с образованием, названием, записью и сравнением долей
Ознакомить детей с долями значит сформировать конкретные представления о долях, т. научить детей образовывать доли практически. Образуем 1/2 долю. Берем круг. – На сколько равных частей надо разделить круг?
Как называется каждая из равных частей?
Сколько таких вторых долей
в целом круге?
Сколько надо взять частей, чтобы
получить 1/2?

Методика ознакомления с образованием, названием, записью и сравнением долей
Для образования ¼ доли можно провести практическую работу с полосками. Аналогично образуем 1/3, 1/5, 1/6, 1/8, 1/10 и т. доли. Для формирования правильных представлений о долях надо использовать достаточное количество наглядных пособий. Название долей происходит одновременно с образованием.

Запись долей
Доли записывают с помощью двух чисел. Например, 1
3
Число под чертой показывает на сколько равных частей разделили круг. Число над чертой показывает сколько таких частей взяли.

Сравнение долей
Сравнение долей происходит практически (на наглядной основе)
1
1/2
1/2
1/4
1/4
1/4
1/4
1/8
1/8
1/8
1/8
1/8
1/8
1/8
1/8

Ознакомление с методикой решения задач на нахождение доли от числа и числа по доле
Задача. От полоски длиной 12 см отрезали 1/3 ее. Чему равна длина отрезанной полоски?
Изобразим полоску в виде отрезка. Чему равна ее длина?
На сколько равных частей
надо разделить полоску?
Сколько таких частей нужно взять?
Какой вопрос задачи?
Как записать решение задачи?
12 : 3 = 4 (см)
Ответ: длина отрезанной полоски равна 4 см. 1
3
?
12 см

Задания на закрепление понятия доли
Объясните, как получить 1/3 долю круга?
Что означает выражение 1/5 отрезка?
Круг разделили на 7 равных частей. Как называется одна такая часть?
Отрезок разделили на 4 разные части. Можно ли одну часть назвать «одной четвертой долей отрезка»?
Назовите, какая доля прямоугольника закрашена и запишите эту долю. Что обозначают в этой записи числа, записанные выше и ниже черты?
6. Найдите 1/4 долю от 1 м, 1/10 от 1 дм. Сколько часов составляет 1/2, 1/4 суток?

Методика ознакомления с образованием, названием и записью дробей
Разделите круг на 4 равные части. Как называется каждая такая часть?
Покажите три четвертых доли. Как получили дробь – три четвертых?
Кто сможет записать эту дробь?
Что показывает число 4?
Что показывает число 3?
Аналогичным образом обучающиеся получают и записывают другие дроби, объясняя, что показывает каждое число.

Сравнение дробей

Ознакомление с методикой решения задач на нахождение дроби от числа
Задача. У монтера было 12 м провода. 2/3 всего провода он израсходовал. Сколько метров провода израсходовал монтер?
Изобразим отрезком кусок провода, приняв 1 см за 1 м. Какой длины отрезок надо начертить?
Что сказано об израсходованном
проводе?
Как изобразить израсходованный
кусок провода?
12 : 3. Что этим узнаем?
Затем результат умножим на 2. Что этим узнаем?
Решение: 12 : 3 2 = 8(м)
Ответ:монтер израсходовал 12 м провода. 2
3
?
12 м

Задания на закрепление понятия дроби
Объяснение образования дробей по готовому рисунку. Запись дробей по готовому рисунку. Изображение дробей с помощью отрезка. (Н-р, покажи 2/5 отрезка). Сравнение дробей, в основном, по изображению равных прямоугольников.

Составные задачи
Позднее задачи на нахождение дроби включаются в составные задачи. В овощной ларек привезли 360 кг капусты. В первый день продали 1/3 часть, во второй – ¾ остатка. Остальную капусту продали в третий день. Сколько килограммов капусты продали в третий день?
360 : 3 = 120 (кг) – продали в первый день
360 – 120 = 240 (кг) – осталось продать
240 : 4 3 = 180 (кг) – продали во второй день
240 – 180 = 60 (кг)
Ответ: 60 кг капусты продали в третий день.

Особенности методики изучения долей и дробей по учебникам Л. Петерсон
Доли изучаются в 4кл. 1), дроби – 4 кл. 1) вводится обобщенная запись доли 1 / n. 2) вводятся правила при сравнении долей. Чем больше долей, тем меньше каждая доля
Чтобы найти 1/ n долю числа, можно разделить это число на n. Чтобы найти неизвестное число, можно его 1/ n долю умножить на n. 3 ) вводятся понятия «числитель» и «знаменатель» дроби;
4) вводится понятие процента;

5) вводятся правила сравнения дробей с одинаковыми числителями и знаменателями. Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше. Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше. 6) Вводятся правила для нахождения части числа и числа по его части. Чтобы найти часть числа, выраженную дробью, надо это число разделить на знаменатель и умножить на числитель дроби. Чтобы найти число по его части, выраженной дробью, надо разделить эту часть на числитель и умножить на знаменатель дроби.

При решении задач используются модели вида:
7) решение задач на проценты;
8) введение темы «Деление и дроби». Задача. 5 пирожных разделили поровну между 12 детьми. Сколько получил каждый?
m : n = m / n
Если m одинаковых предметов разделить на n равных частей, то каждая часть будет равна m / n целого предмета. 9) введение формул сложения и вычитания дробей;
1 – 24 уч. 1
4
– ? уч.

10) правильные и неправильные дроби;
Запиши с помощью дробей число четвертых долей круга на рисунках. Какие из полученных дробей больше 1, меньше 1, равны 1?
а) б) в)
г) д)
Отметь на числовом луче дроби 1/4,, 2/4,3/4, 4/4, 5/4, 6/4, 7/4, 8/4, 11/4, 12/4. Какие из отмеченных дробей правильные, а какие неправильные?

11) смешанные числа
12) выделение целой части из неправильной дроби. 13) сложение и вычитание смешанных чисел. Чтобы сложить смешанные числа, надо сложить отдельно их целые и дробные части. 0
1
2
2
3
7/3
67
12
60
5
7
целая часть
знаменатель
числитель
1
3

Программа «Школа 2100»

УМК “Гармония» 4 кл
Какая часть прямоугольника закрашена на каждом рисунке?
Миша: Я думаю, что на каждом рисунке закрашена одна часть прямоугольника. Маша: По-моему, ты не понял, о чем тебя спрашивают и отвечаешь на вопрос: «Сколько частей прямоугольника закрашено на каждом рисунке?» Посмотрите внимательно, чем прямоугольники отличаются друг от друга?. Ведь каждый из них разделили по-разному на равные части.

Миша: Действительно, первый разделен на 15 частей, второй на 6 равных частей. Я кажется, догадался! По-моему, на первом рисунке закрашена 1/15 часть прямоугольника, на втором – 1/6 прямоугольника и т. Но как это записать математическими знаками?
Маша: Для этого математики придумали числа, которые назвали дробями. Задания:
выбор решения;
выбор схемы;
выбор рисунка;
сравнение рисунков и др.


Отрезок АВ имеет длину 12 см. Начерти

Выбери рисунок, которому соответствует каждая дробь и объясни, что она обозначает 2/6, 3/4,5/7, 8/9, 1/4, 1/9, 2/7, 4/6.

Составьте задание к данному рисунку.

2)
2. 4)
3. 1)
4. 3)
5. 1)
6. 3)
7. 1)
8. 1)
9

Задания для внеаудиторной самостоятельной работы
Подберите или составьте по 2 задачи на нахождение дроби от числа и числа по его дроби. Постройте модель к каждой из них и запишите решение. Составьте математический диктант по теме «Доли и дроби». Составить разноуровневые задания по теме «Нахождение дроби от числа и числа по его дроби» (по 3 задания каждого уровня). Ознакомьтесь с конспектом урока по математике, разработанном в технологии модульного обучения по теме «Доли и дроби».

Вторник, 21 января 2020 г.
Доброго времени суток уважаемые студенты 21 КП!
Вашим домашнее заданием было изучение ФГОС НОО. После изучения данного материала вам необходимо пройти тестирование
Составьте краткий конспект лекции.
Какими знаниями, умениями, навыками должны обладать выпускники детского сада?
С помощью каких заданий можно проверить математическую готовность ребенка к школе?
Какие основные требования к математической подготовке по окончанию начальной школы?
В чем заключается преемственность изучения математики детский сад — начальная школа — средняя школа?
Подберите диагностики математической готовности к школе.
Пятница, 2 марта 2018 г.
Уважаемые 41 КП!
Поздравляю Вас с окончанием изучения методики преподавания математики! Надеюсь, что вы покажете высокий уровень своих знаний при сдаче комплексного экзамена по модулю.
Для выполнения последней практической работы воспользуйтесь ссылкой
Изучите объем изучения величины время в начальной школе
Вторник, 27 февраля 2018 г.
Уважаемые студенты группы 41 КП!
Четверг, 8 февраля 2018 г.
Уважаемые студенты 21 КП!
Изучите типичные ошибки возникающие у школьников при изучении вычислительных приемов, формировании вычислительных навыков.
Выпишите ошибки и задания по их устранению. Повторите материал предыдущих сообщений из раздела «Вычислительные приемы»
Вторник, 6 февраля 2018 г.
Очень скоро вас ждет квалификационный экзамен, необходимо начать подготовку к нему. Ознакомьтесь с заданиями
Понедельник, 29 января 2018 г.
Доброго времени суток 41 КП!
Одной из самых важных тем в курсе изучения математики является тема «Решение задач на построение». Так же данная тема является одной из самых трудных, в связи с слабо сформированными навыками решения задач данного вида самими педагогами. Поэтому вы должны уделить изучению данной темы особое внимание.
Дайте ответы на вопросы:
1. В чем заключаются задачи изучения геометрического материала в началь ных классах
2. Что является решением задачи на построение?
3. Что обозначает найти решение задачи на построение?
4. Что обозначает решить задачу на построение?
5. Перечислите элементарные задачи на построение. Какие из элементарных задач на построение изучаются в начальной школе?
7. Дайте краткую характеристику этапам решения задач на построение. Дайте характеристику видам задач на построение изучаемые в начальной школе.
Четверг, 8 февраля 2018 г.
Доброго времени суток уважаемые студенты 21 КП.
Tomsmetodikoy. blogspot. com
Тесты по курсу «Методика преподавания математики младшим школьникам»
4) средством развития приемов умственной деятельности.
Процесс обучения математике младших школьников является __________Науки «Теория и технологии начального математического образования»:
Ядром − компонентами методической системы обучения математике являются цели, содержание, обучения, __________________________________________и взаимосвязи между ними:
3) организационные формы;
4) 1, 2, 3.
Из скольких основных компонентов состоит разработанная А. Пышкало методическая система обучения математике:
1) пяти;3) четырех;
В примерной программе по начальному курсу математики (ФГОС-2) отдельным разделом не представлен:
1) арифметический материал;
2) материал о величинах;
Алгебраический материал.
4) геометрический материал;
Из шести разделов рекомендуемой разработчиками ФГОС-2 примерной программы по математике для начальных классов на основе содержания всех других изучается раздел:
1) «Числа и величины»;
2) «Арифметические действия»;
3) «Текстовые задачи»;
4) «Пространственные отношения. Геометрические фигуры»;
5) «Геометрические величины»;
Работа с информацией».
Установите соответствие между понятием и компонентом содержания начального математического образования.
1) натуральные числа; а) арифметика;
2) площадь; б) величины;
3) угол; в) элементы геометрии;
4) равенство; г) элементы алгебры;
5)Таблица; д) работа с информацией.
Изучение математики в начальной школе направлено на достижение следующих целей:
1) математическое развитие младших школьников;
2) освоение начальных математических знаний и умений применять их в решении учебных, познавательных и практических задач;
3) воспитание интереса к математике, стремления использовать математические знания в повседневной жизни;
Математическое развитие обучающихся в начальных классах не предусматривает:
1) совершенствование вычислительной культуры младших школьников;
2) формирование способности к интеллектуальной деятельности;
3) развитие пространственного мышления и математической речи;
4) формирование умения вести поиск информации (фактов, оснований для упорядочения, вариантов и др.
Метапредметными результатами изучения математики младшими школьниками не являются:
1) умения анализировать учебную ситуацию с точки зрения математических характеристик, устанавливать количественные и пространственные отношения объектов окружающего мира;
2) освоенные знания о числах и величинах, арифметических действиях, геометрических фигурах;
3) способность моделировать и определять логику решения практической и учебной задачи;
4) умения планировать, контролировать, корректировать ход выполнения заданий.
Укажите неправильный ответ.
Формы обучения математике в начальных классах включают в себя:
2) домашнюю работу учащихся;
3) работу со счетным материалом;
Укажите верное суждение:
1) внеурочная работа — это обязательные систематические занятия педагога с учащимися в свободное от основных занятий время;
2) урок − это основная форма обучения младших школьников математике;
3) к видам внеклассной работы относятся: домашняя работа учащихся, групповая работа, фронтальная работа;
4) основными методами обучения младших школьников математике являются наблюдение и эксперимент.
Установите последовательность этапов урока открытия нового:
1) постановка учебной задачи; 2 этап;
2) открытие нового знания; 3 этап;
3) самостоятельная работа с самопроверкой; 5 этап;
4) первичное закрепление; 4 этап;
5) актуализация опорных знаний. 1 этап.
Тип и структура урока математики в начальной школе не определяются:
1) дидактическими задачами урока;
2) местом урока в системе уроков по теме;
3) местом урока в расписании;
4) степенью освоения учащимися содержания учебной темы.
Установите соответствие между этапом урока открытия нового знания и его дидактической целью.
1) открытие нового знания;

2) самостоятельная работа с самопроверкой;
3) актуализация опорных знаний;
А) проектирование и фиксация нового знания;
Б) формирование навыков самоконтроля и самооценки;
В) содержательная и мыслительная подготовка;
Г) рефлексия деятельности.
Основной формой обучения математике в начальных классах является:
2) домашняя работа учащихся;
3) внеурочная работа по математике;
К систематическим видам внеурочной работы по математике относится:
2) кружковая работа и факультативные занятия;
3) математический утренник;
4) выпуск математической газеты.
Укажите неверный ответ. Домашняя работа по математике в начальной школе:
1) является формой самостоятельной работы учащихся;
2) подлежит обязательной проверке учителем или самопроверке;
3) Содержит задания только занимательного характера;
4) направлена на тренировку учащихся в известных способах действий.
Функциями учебника как основного средства обучения математике в начальной школе являются:
Укажите неправильный ответ. Содержание начального курса математики построено на следующих принципах:
3) связи теории и практики;
4) на органичном соединении арифметики, алгебры и геометрии.
Построение начального курса математики на системе целесообразно подобранных задач предложил:
1) С. Шохор-Троцкий;
Укажите номер неверного ответа.
Выделите функции дидактической игры в процессе обучения математике:
2) обоснование теоретической основы вычислительного приема;
4) воспитание интереса к математике.
К какому из компонентов методической системы относятся дидактические игры:
1) средства обучения;
2) методы обучения;
3) организационные формы;
4) содержание обучения.
«Сложение и вычитание многозначных чисел выполняется так же, как и трехзначных». Это рассуждение:
3) по аналогии;
При ознакомлении с понятием «квадраты» для выявления существенных признаков этого понятия учитель предложил распределить прямоугольники на две группы. На какой логической операции основан использованный учителем методический прием?
При оценивании устного выполнения вычислений не учитывается один из следующих критериев:
Аккуратность записи решения.
Результативность изучения математики выпускниками начальной школы и их готовность к обучению в 5-м классе определяется:
1) итоговой контрольной работой по математике;
2) комплексной проверочной работой;
3) портфолио успехов по математике обучающихся за 1-4 классы;
Итоговая контрольная работа по математике в 4-м классе содержит 3 группы заданий (выдели неверный ответ):
1) задания игрового или занимательного характера;
2) задания базового уровня сложности;
3) задания повышенной сложности двух видов;
Оценка результатов выполнения итоговой за учебный год контрольной работы осуществляется в баллах:
1) по 5-ти бальной шкале с учетом количества допущенных учеником ошибок и недочетов;
2) по 3-х бальной шкале с учетом рекомендаций разработчиков заданий для контроля;
3) по 2-х (0, 1 балл) или 3-х (0, 1, 2 балла) шкалам, при этом подсчитывается суммарный балл, полученный за все задания;
4) способ оценивания может выбрать учитель, ориентируясь на индивидуальные особенности ученика.
К средствам обучения математике в начальных классах не относятся:
1) учебники и тетради на печатной основе;
2) наглядные печатные пособия;
3) экскурсии, групповая работа над проектом;
4) компьютеры, проекторы и цифровые образовательные ресурсы.
При использовании в обучении младших школьников математике компьютерных программ (презентаций, информационно-обучающих, тестирующих) необходимо предусматривать:
1) ограничение применения ИКТ во времени;
2) смену видов деятельности обучающихся на уроке;
3) организацию валеологических пауз;
4) верно 1, 2, 3;
5) достаточно 1 и 2.
Применение компьютерных технологий на уроках математики в начальных классах целесообразно, поскольку создается возможность (укажи неверное):
1) демонстрировать реальные объекты и процессы как учебный материал для построения математических моделей окружающей действительности;
2) организовывать подвижные игры как динамические паузы;
3) осуществлять оперативный контроль и мониторинг овладения обучающимися математическими знаниями и умениями;
4) при необходимости вести поиск информации.
Установите соответствие между названием учебно-методического комплекта и фамилией автора учебников математики в этом УМК:
1) «Начальная школа ХХI века»;А) В. Рудницкая;
2) «Планета знаний»;Б) М. Башмаков, М. Нефедова;
3) «Гармония»;В) Н. Истомина;
4) «Школа России»;Г) М. Моро и др
5) «Перспектива»; д) Л. Петерсон
Согласно требованиям стандартов второго поколения в содержании начального курса математики выделен новый раздел:
1) «Работа с информацией»;
2) «Числа и величины»;
3) «Арифметические действия»;
4) «Текстовые задачи».
Раздел программы начального курса математики «Работа с информацией», изучаемый на основе других разделов данного курса, преследует цели — научить младших школьников ( выделите главное):
1) «читать» таблицы и организовывать информацию в таблицах;
2) работать с диаграммами;
3) вести поиск информации для разрешения проблемы или выполнения задания;
Верно 1 и 2?
Цели дифференциации понятий число и цифра не послужит:
1) задание на запись чисел заданными цифрами;
2) изучение понятий однозначное и двузначное числа;
3) знакомство с римской и славянской нумерацией;
4) чтение стихов о цифрах.
В курсе математики Н. Истоминой числа первого десятка изучаются не по порядку, а по принципу схожести и трудности написания цифр. Данный подход предусматривает формирование:
1) порядкового натурального числа;
2) натурального числа как меры величин;
3) Количественного натурального числа;
4) натурального числа как результата счета и измерения.
С целью формирования представлений о десятке как новой счетной единице проводятся упражнения на:
1) счет однородных предметов группами по 2, 3, 4, 5, …, 10 элементов в каждой группе;
2) измерение длин отрезков с помощью дециметра;
3) решение примеров вида: а + b= 10;
4) нет верного ответа.
В изучении нумерации чисел первой сотни в учебниках М. Моро и др. выделяют следующий порядок:
1) Устная и письменная нумерация чисел 11-20, устная и письменная нумерация чисел 21-100;
2) устная нумерация чисел 11-20 и 21-100, письменная нумерация чисел 11-20 и 21-100;
3) устная нумерация чисел 11-20 и 21-100, письменная нумерация двузначных чисел;
4) изучение устной и письменной нумерации чисел 11-20 и 21-100 ведется параллельно.
Почему при изучении нумерации чисел в концентре «Сотня» целесообразно выделить этап «Числа от 11 до 20»:
1) образование чисел от 11 до 20 рассматривается присчитыванием по 1 аналогично обра-зованию чисел первого десятка, а числа 21-100 образуются из десятков и единиц;
2) Структура названия чисел 11-20 отличается от структуры названия чисел 21-100: различен порядок называния и записи разрядных единиц;
Незнание алгоритма.
Определите тип задачи с тройкой пропорционально связанных величин: «На клумбе высадили 60 луковиц тюльпанов и 40 луковиц нарциссов в одинаковые ряды. Всего получилось 10 рядов. Сколько рядов занято тюльпанами и нарциссами в отдельности?»
1) на нахождение четвертого пропорционального;
2) на нахождение неизвестного по двум разностям;
3) не является типовой задачей;
4) На пропорциональное деление.
Верно 1 и 4?
Какие методические приемы используются в начальном изучении математики при ознакомлении с конкретной величиной:
1) ознакомление с аксиомами, характеризующими величину;
2) практическая работа для сравнения предметов по различным признакам, выделение определенного признака, установление отношений больше, меньше или равно по этому признаку;
3) введение названия величины с опорой на дошкольный опыт обучающихся, обозначающего определенный признак предметов окружающей действительности;
4) рассмотрение исторических сведений об измерении величины;
Верно 2 и 3?
Какие методические приемы используются в начальном изучении математики для расширения знаний о величинах:
1) ознакомление с аксиомами, характеризующими величину;
2) практическая работа для установления отношений больше, меньше или равно между предметами окружающей действительности по определенному признаку;
3) поиск в сети «Интернет» или книгах сведений о природных объектах, которые выражены значениями величин, характеризующих их размеры, массу и др
4) рассмотрение исторических сведений об измерении величин;
Верно 3 и 4?
Какие методические приемы используются в начальном изучении математики при формировании умения применять знания и умения о величинах в практических ситуациях и в познавательных целях:
1) практическая работа для установления отношений больше, меньше или равно между предметами окружающей действительности по определен-ному признаку;
2) поиск в сети «Интернет» или книгах сведений о природных объектах, которые выражены значениями величин, характеризующих их размеры, массу и др
3) рассмотрение исторических сведений об измерении величин;
4) составление и решение текстовых задач на основе данных об объектах природы, быта и др. , о процессах взвешивания, работы, движения и др. , обсуждение значений величин, полученных при решении задач;
Верно 2 и 4?
Какие из методических приемов не используются в начальных классах при изучении величин:
1) ознакомление с аксиомами, характеризующими величину;
2) практическая работа для установления отношений больше, меньше или равно между предметами окружающей действительности по определенному признаку;
3) поиск в сети «Интернет» или книгах сведений о природных объектах, которые выражены значениями величин, характеризующих их размеры, массу и др
4) сравнение предметов окружающей действительности по определенному признаку;
5) рассмотрение исторических сведений об измерении величин?
На каком уровне изучаются «величины» в начальных классах:
1) на теоретическом уровне;
2) на уровне общих представлений и практического применения знаний и умений;
3) на понятийном уровне;
Найдите утверждения, подтверждающие, что площадь — это величина:
1) площадь имеют только многоугольники;
2) площадь можно измерить и выразить результат измерения числом;
3) площадь — это место в городе, где проводятся праздники;
4) площадь характеризует свойство предмета занимать место на плоскости (поверхности);
Верно 2 и 4.
Установите последовательность этапов работы над определенной величиной:
А)опосредованное сравнение носителей величины с помощью условной мерки;
Б)введение стандартной единицы измерения для данной величины;
В) непосредственное сравнение предметов по определенному свойству, характеризующему величину;
Г) сравнений числовых значений величины, выполнение арифметических действий с ними;
1) в, а, б, г;
Установите последовательность приемов организации работы над определенной величиной:
А)знакомство с измерительными инструментами (линейкой, палеткой и др. ), тренировка в измерении величин;
Б) сравнение величин визуально, с помощью мускульных усилий, наложением;
В)сравнение, сложение, вычитание однородных величин, умножение и деление величины на число, нахождение кратного отношения величин;
Г) измерение величин различными мерками, исследование взаимосвязи между единицей измерения величины и ее числовым значением;
Б, г, д, а, в.
Пониманию младшими школьниками взаимосвязи между понятиями: число и величина не способствует:
1) ознакомление с историческими сведениями о величинах;
2) упражнения в измерении величин;
3) построение отрезка по заданной его длине;
4) построение прямоугольника по его перимеру или площади;
5) выполнение заданий на установление соответствия между величиной и её числовым значением.
Укажите неверное утверждение. Ознакомление младших школьников со старинными единицами измерения величин (ладонь, локоть, сажень, пуд, фунт и др. ) дает учителю возможность:
1) расширить кругозор обучающихся и воспитывать у них интерес к математике;
2) обосновать необходимость введения стандартных (общепринятых) единиц измерения;
3) формировать умение работать на уроках математики в парах и группах;
4) проиллюстрировать прикладную направленности начального курса математики.
Укажите неверное утверждение. Обучающиеся выполняют измерение величин с помощью различных мерок с целью:
1) осознания зависимости между меркой и числом, полученным в результате измерения;
2)развития практических умений измерять величины;
3) формирования умений работать в группах;
4) осознания необходимости выбора единой (общепринятой)единицы измерения конкретной величины.
Укажите несущественное. Для формирования умения измерять величины младший школьник должен знать:
1) таблицу мер каждой из величин;
2) каким именно прибором измеряют данную величину;
3) шкалу прибора и правила работы с ним;
Верно 1, 2 и 4.
Первые представления о форме, размерах и взаимном расположении предметов в пространстве дети получают:
1) в дошкольный период развития математических представлений;
2) с первыхдней обучения ребенка в школе;
3)на внеурочных занятиях;
4) в ходе проектной деятельности;
5) в четвертом классе.
Каким геометрическим понятиям даются определения в курсе математики начальной школы:
1) круг и окружность;
2) Прямоугольник и квадрат;
3) угол и многоугольник;
4) длина и площадь?
Первоклассникам розданы карточки с изображением различных многоугольников. С какой целью учитель предложил задание: « Раскрасьте все треугольники. Посчитайте, сколько сторон, вершин, углов у треугольника»:
1) формирование понятия, что форма фигуры не зависит от материала, из которого она изготовлена.
2) выявление существенных и несущественных признаков треугольника;
3)развивать умения анализировать геометрические фигуры, сравнивать, классифицировать и т
Верны утверждения 2 и 3.
5) верны утверждения 1,2 и 3?
Укажите среди утвержденийневерные. При формировании представлений о прямой линии у первоклассников полезно решать следующие задачи:
1) сравнивать прямую и кривую линии;
2) ставить точки на прямой и вне прямой линии, устанавливать положение точки относительно заданной прямой линии;
3) проводить прямые и кривые линии через 1,2,3 заданные точки;
Верно 1 или 2.
Умение находить периметр многоугольника предполагает владение обучающимся следующими умениями:
1) находить длину ломаной линии; 2) пользоваться линейкой;
3) измерять стороны многоугольника;
4) вычислять сумму нескольких чисел – значений величин;
5) все ответы верны.
Обучающиеся в начальных классах усваивают понятие Периметр только на примере многоугольника: «Периметр многоугольника – это сумма длин всех его сторон». В чем ограниченность такого подхода к изучению периметра:
1) не отражается общее то, что периметр – это длина границы любой плоской геометрической фигуры;
2) не содержится информация о возможности и способе нахождения периметра круга и других фигур, ограниченных кривой замкнутой линией;
3) нет верного ответа; 4) верны 1 и 2 утверждения.
Периметр24 см24 см…
Длина
Ширина
Обучающимся в третьем классе предложено задание: «Сколько можно построить прямоугольников с периметром 24 см, длина и ширина которых выражается натуральными числами? Заполните таблицу».
Каковы учебные задачи этого задания:
1) актуализация понятия периметр;
2) применение правила нахождения периметра прямоугольника; 3) обучение построению прямоугольников;
4) обучение младших школьников работать с информацией;
5) связь теории и практики в обучении математике;
Тесты по курсу «Методика преподавания математики младшим школьникам»
3 внеурочная работа по математике;.
Геометрические понятия в начальной школе
Одной из основных задач изучения геометрического содержания в курсе математики начальной школы является развитие пространственного воображения у ребенка, умения наблюдать, сравнивать, обобщать, анализировать и абстрагировать. Второй важной задачей является формирование у ребенка практических умений измерения и построения геометрических фигур с помощью циркуля, угольника и линейки. Задания на вычисления различных параметров геометрических фигур (длин отрезков, периметра и площади прямоугольника и квадрата) позволяют показать ребенку взаимосвязь количественных и пространственных характеристик объектов материального мира, а также показать еще одно приложение понятия «натуральное число» —»как результата измерения величин.
В соответствии с последней редакцией Обязательного минимума содержания образования по математике для начальных классов список изучаемых геометрических понятий значительно расширился по отношению к предыдущим вариантам стабильной программы. Общая тенденция геометризации курса школьной математики коснулась и начальных классов. В соответствии с этой тенденцией насыщение курса математики начальной школы геометрическим содержанием является перспективной линией развития математического образования начального звена.
Обязательный минимум содержания образования по математике содержит следующий перечень понятий геометрического характера:
Точка. Линии: прямые, кривые. Отрезок. Угол. Прямой угол. Многоугольники: треугольник, прямоугольник, квадрат. Вершины и стороны многоугольника. Окружность и круг. Куб. Шар.
Измерение площади. Вычисление площади прямоугольника.
По отношению к этому перечню, определяющему минимум содержания, сегодняшний традиционный учебник математики содержит намного больше геометрических понятий. Можно отметить, что сегодня стабильный учебник математики содержит даже больше геометрических понятий, чем многие альтернативные учебники развивающих систем.
Геометрические понятия в начальной школе
В 1 классе различные геометрические фигуры используются как материал для построения заданий на распознавание, сравнение, обобщение и классификацию. Цель этих заданий — формирование и развитие наблюдательности ребенка; формирование и развитие умения выделять существенные (важные) признаки предмета, умения сравнить два или несколько предметов, отмечая при этом сходные и различные признаки и свойства; умения сделать несложное обобщение на основе выделенных общих свойств предметов; умения распределять предметы на группы (классификация) в соответствии с выделенным признаком.
Такие задания являются основными для формирования и развития мыслительных операций (анализ, синтез, сравнение, классификация и др. ), а также умения строить обоснованные (логические) рассуждения. Необходимость обучать детей всем этим умениям оговорена в Обязательном минимуме содержания образования для начальной школы в разделе «Требования к уровню подготовки выпускников начальных классов» (М. , 2001).
Геометрические понятия, с которыми дети знакомятся в 1 классе:
Точка. Линия — кривая и прямая. Отрезок. Ломаная. Звенья ломаной. Вершина ломаной. Замкнутая и незамкнутая ломаная. Многоугольники. Треугольники и четырехугольники.
Точка — неопределяемое понятие геометрии. С точкой обычно знакомят методом показа — рисуют или прокалывают стержнем ручки в листочке бумаги. Считается, что точка не имеет ни длины, ни ширины, ни площади.
Линия — неопределяемое понятие геометрии. С линией знакомят методом показа — моделируют из шнура, или рисуют на доске или на листе бумаги.
Прямую линию удобно моделировать, сгибая любой лист бумаги — линия сгиба всегда прямая. Основное свойство прямой линии: прямая линия бесконечна.
Кривую линию удобно моделировать из шнура. Кривая линия также бесконечна (если она не замкнутая).

Ломаную линию удобно моделировать, используя счетные палочки или складной металлический метр. Ломаная линия содержит конечное число звеньев. Звено ломаной — отрезок. Точки соединения концов звеньев называют — вершинами ломаной. Звенья ломаной должны быть соединены последовательно.

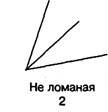
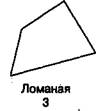
В программе 1 класса линии рассматривают только на плоскости.
Основные взаимоотношения точки и прямой или кривой линии, с которыми знакомятся дети в 1 классе:
Через одну точку можно провести множество прямых.
Через одну точку можно провести множество кривых.
Через две точки можно провести только одну прямую.
Через две точки можно провести множество кривых.
Отрезок — часть прямой, заключенная между двумя точками.
Отрезок имеет определенную длину, которую можно измерить.
Линейка — инструмент для измерения длин отрезков.
Ломаная и кривая линии могут быть замкнутыми и незамкнутыми. На рисунке ломаная 1 — незамкнутая, ломаная 3 — замкнутая.
Замкнутая ломаная на плоскости ограничивает многоугольник.
Многоугольник — плоская фигура, ограниченная замкнутой ломаной.
Треугольник — ограничен ломаной из трех звеньев. Соответственно имеет три стороны и три вершины.
Четырехугольник — ограничен ломаной из четырех звеньев. Соответственно имеет четыре стороны и четыре вершины.
Геометрические понятия, с которыми дети знакомятся во 2 классе: Длина ломаной. Прямой угол. Непрямой угол. Прямоугольник. Квадрат.
Длина ломаной — сумма длин звеньев ломаной. Для нахождения длины ломаной следует измерить длину каждого звена и результаты сложить.
Прямой угол — это угол, который по определению содержит 90°. Поскольку в начальной школе при обучении по стабильной программе дети не знакомятся с градусной мерой углов, понятие прямого угла дается методом показа:
Для получения модели прямого угла дети используют лист бумаги, сгибая его соответствующим образом:
Прямой угол
Методом проб дети учатся находить прямой угол среди рисунков других углов и на различных геометрических фигурах: прикладывают к ним свою модель, выделяя углы, с ней совпадающие. Модель прямого угла служит средством проверки такого выбора. В дальнейшем бумажная модель прямого угла заменяется угольником, который является основным инструментом для распознавания и построения прямых углов.
Прямоугольник — четырехугольник, у которого все углы прямые. Основное свойство прямоугольника: противолежащие стороны прямоугольника имеют равные длины.
Это свойство дети определяют опытным путем: перегибают бумажные модели прямоугольников, совмещая противолежащие стороны.
При невозможности применить этот метод, его заменяют измерением длин противолежащих сторон.
Используя это свойство, дети должны уметь чертить прямоугольник по известным длинам двух его сторон, понимая, что две другие стороны имеют такие же длины, а углы его — прямые.

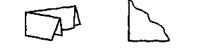
Квадрат — прямоугольник, у которого все стороны равны.
Используя это определение, дети должны уметь чертить квадрат по известной длине одной стороны, понимая, что все остальные стороны квадрата имеют такую же длину, а углы его — прямые.
Геометрические понятия, с которыми знакомятся в 3 классе:
Периметр многоугольника. Площадь прямоугольника. Круг. Окружность. Радиус. Диаметр. Треугольники равносторонние, равнобедренные и разносторонние.
В 3 классе дети знакомятся с обозначением фигур заглавными латинскими буквами.
Чтобы назвать отрезок, обозначают точки, которые являются его концами.
Чтобы назвать многоугольник, обозначают буквами его вершины. Например: квадрат АВСD.

Чтобы назвать ломаную, также обозначают буквами ее вершины. Например: ломаная РКЕB.
Периметр многоугольника — сумма длин всех его сторон. Для нахождения периметра многоугольника измеряют длины его сторон и складывают полученные результаты.
Периметр квадрата находят умножением на 4 длины его стороны, поскольку стороны квадрата имеют равные длины.
Площадь плоской фигуры измеряется количеством стандартных мер площади, укладывающихся внутрь фигуры. Стандартные меры площади: мм²; см²; дм²; м²; км².
В 3 классе дети знакомятся с см².
Инструмент для определения площади всех фигур — палетка.
Палетка — лист кальки (или прозрачного пластика), на который нанесена сетка квадратов размером 1 см х 1 см. Для измерения площади фигуры с помощью палетки, ее накладывают на фигуру

Способ нахождения площади прямоугольника: Чтобы вычислить площадь прямоугольника, измеряют его длину и ширину (в одинаковых единицах) и находят произведение полученных чисел.
От прямоугольного листа со сторонами 5 см и 3 см отрезали полоску со сторонами 3 см и 1 см. Найди площадь оставшейся части.
Найдем площадь данного листа: 5 см • 3 см = 15 см².
Найдем площадь полоски: 3 см • 1 см = 3 см².
Найдем разницу площадей: 15 см² — 3 см² =12 см². Используя чертеж, данную задачу можно решить другим способом:
Анализ рисунка сразу показывает, что оставшаяся часть имеет площадь: 3 см • 4 см = 12 см².
Окружность и круг образованы замкнутой кривой линией. Круг — часть плоскости, ограниченная окружностью. Граница круга — окружность.
Поскольку в начальных классах не знакомят детей с классическим определением окружности (множество точек, равноудаленных от центра), знакомство с окружностью проводят методом показа, связывая его с непосредственной практической деятельностью по вычерчиванию окружности при помощи циркуля. Замкнутая кривая линия, которую рисует грифель циркуля — это окружность. Окружность (круг) имеет центр: точка О — центр окружности (круга).
Радиус окружности — отрезок, соединяющий центр окружности с какой-нибудь ее точкой. Например: ОМ — радиус окружности (круга). Основное свойство радиусов одной окружности: Радиусы одной окружности (круга) равны.
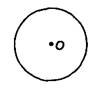
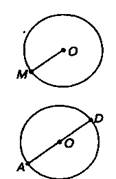
Диаметр окружности (круга) — отрезок, проходящий через центр окружности (круга) и соединяющий две любые ее точки.
Например: диаметр АО.
Основное свойство диаметров одной окружности (круга): Диаметры одной окружности (круга) равны.
Отношения между радиусом и диаметром одной окружности (круга): Диаметр равен двум радиусам.
Треугольники, имеющие стороны разной длины, называют разносторонними.
Треугольники, у которых равны две стороны, называют равнобедренными.
Среди равнобедренных треугольников есть такие, у которых равны все три стороны. Эти треугольники называют равносторонними.
Геометрические понятия, с которыми дети знакомятся в 4 классе:
Диагонали прямоугольника. Свойства диагоналей прямоугольника.
Луч. Числовой луч.
Угол. Элементы угла. Прямой, острый и тупой угол. Треугольники остроугольные, прямоугольные и тупоугольные.
Диагональ многоугольника — отрезок, соединяющий противолежащие вершины многоугольника.
С диагоналями прямоугольника детей знакомят методом показа:
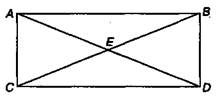
Отрезки АЕ и С — диагонали прямоугольника АВDС.
Точка Е — точка пересечения диагоналей.
Основные свойства диагоналей прямоугольника:
Диагонали АD и В С имеют равные длины.
Отрезки, получаемые при пересечении диагоналей прямоугольника, равны.
Данные свойства определяются эмпирическим (опытным) путем — измерением длин соответствующих отрезков.
Поскольку квадрат является прямоугольником, то его диагонали обладают теми же свойствами. Кроме того, диагонали квадрата пересекаются под прямым углом.
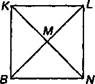
Непосредственное измерение углов с помощью угольника показывает, что углы, получающиеся при пересечении диагоналей квадрата, прямые.
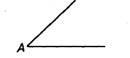
Луч — часть прямой, ограниченная с одной стороны.
Луч имеет начало, но не имеет конца.
Точка А — начало луча.
В математике луч обычно обозначается двумя буквами, например: луч АС. Такая запись обозначает, что луч имеет началом точку А и «идет» в сторону, обозначенную буквой С:
Числовой луч — луч, на котором точками обозначены натуральные числа. Расстояние между точками равно 1 единице измерения (единичный отрезок), которая задается условно. Чаще всего это 1 или 2 клетки.
Каждой точке ставится в соответствие число, начиная с числа 1. Началу луча ставится в соответствие число 0.
Числовой луч играет большую роль при иллюстрации понятия натуральный ряд чисел, позволяет сравнивать натуральные числа, ориентируясь на их расположение на числовом луче, позволяет выполнять приемы присчитывания и отсчитывания по частям с опорой на числовой луч. В связи с этим некоторые альтернативные учебники (Н. Истомина) знакомят детей с этим понятием еще в 1 классе.
Другая роль числового луча состоит в том, что используя это понятие, можно познакомить детей с прямоугольной системой координат (числовой или координатный угол), отрицательными числами (числовая прямая).
Объясни с помощью числового луча, в какую сторону от точки, соответствующей точке 8, надо двигаться, чтобы найти все числа, которые меньше числа 8, и те числа, которые больше, чем 8.


Ответ: Чтобы найти все числа, которые меньше, чем 8, нужно двигаться влево от числа 8. Чтобы найти числа, которые больше, чем число 8, нужно двигаться от него вправо.
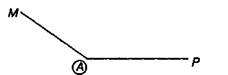
Угол — это фигура, образованная двумя лучами, имеющими общее начало.
Стороны угла — это лучи, образующие угол.
Вершина угла — это общее начало лучей, образующих угол.
Обозначение угла: угол может быть назван по его вершине — угол М; угол может быть назван тремя буквами — угол МАР, при этом буква, стоящая в вершине угла, должна быть средней.
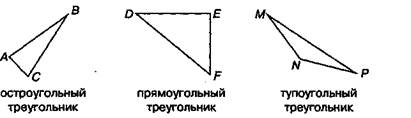
Остроугольный треугольник — треугольник, все углы которого острые.
Прямоугольный треугольник имеет один прямой угол. Тупоугольный треугольник имеет один тупой угол. Например:
В треугольнике не может быть более одного прямого угла.
В треугольнике не может быть более одного тупого угла.
Равносторонний треугольник может быть только остроугольным.
Прямоугольный и тупоугольный треугольники могут быть равнобедренными.
Разносторонними могут быть и остроугольный, и прямоугольный, и тупоугольный треугольники.
Через одну точку можно провести множество прямых.
 Моя школа в online
Моя школа в online